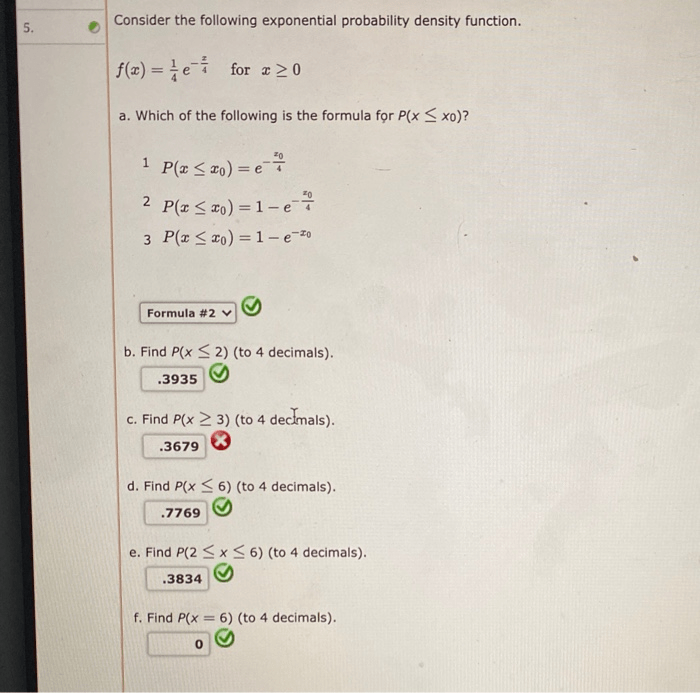
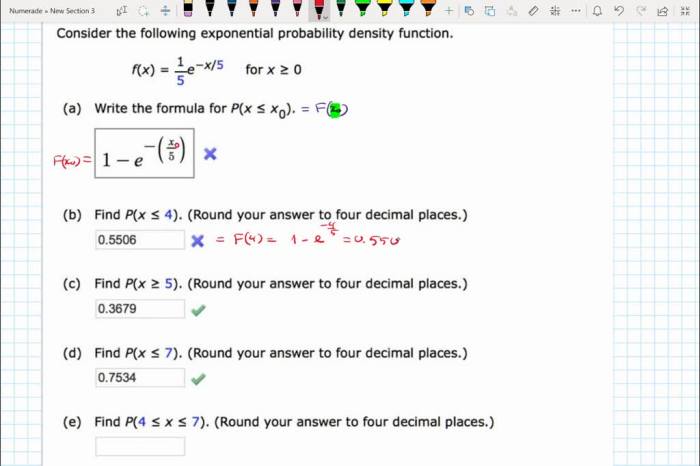
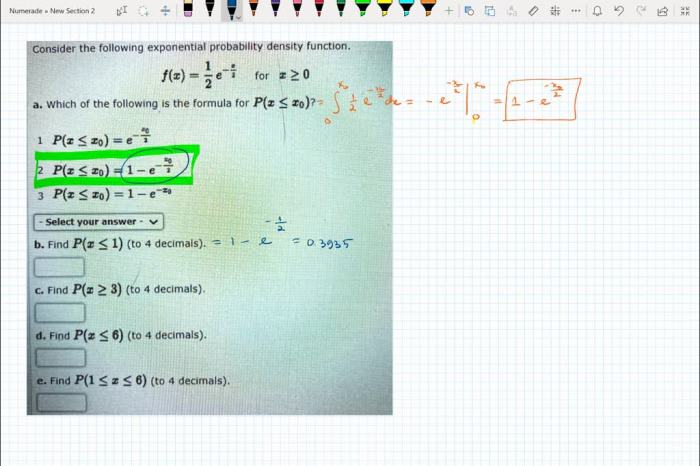
Consider the following exponential probability density function. for – Consider the following exponential probability density function for a deeper understanding of its concept, properties, and applications. This function, denoted by f(x), is a fundamental tool in probability theory and statistical modeling, providing insights into various real-world phenomena.
The exponential probability density function is defined mathematically as f(x) = λe^(-λx), where λ is a positive constant known as the rate parameter. It describes the distribution of random variables that exhibit a constant failure rate, making it particularly useful in reliability engineering and queuing theory.
Exponential Probability Density Function

The exponential probability density function (EPDF) is a continuous probability distribution that describes the time between events that occur randomly and independently at a constant average rate.
Mathematical Formula, Consider the following exponential probability density function. for
The EPDF is given by the following formula:
f(x) = (1/θ) – e^(-x/θ)
where:
- x is the random variable (time between events)
- θ is the mean (average time between events)
- e is the base of the natural logarithm (approximately 2.71828)
Properties
The EPDF has the following properties:
- The mean is θ.
- The variance is θ 2.
- The standard deviation is θ.
- The shape of the distribution is exponential, with a rapid decrease at first and a long tail.
Q&A: Consider The Following Exponential Probability Density Function. For
What is the mean of the exponential probability density function?
The mean of the exponential probability density function is 1/λ.
What is the variance of the exponential probability density function?
The variance of the exponential probability density function is 1/λ^2.
What is the standard deviation of the exponential probability density function?
The standard deviation of the exponential probability density function is 1/λ.